ボケ質は無視して、ボケ量について(ある程度)定量的に考えた。
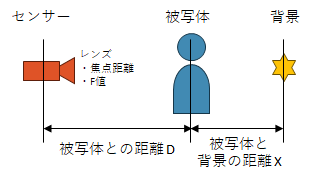
センサー上での錯乱円の大きさは以下で計算できるものとする。
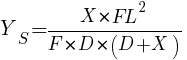
ここで
Ys:センサー平面上での錯乱円の径 [mm]
FL:焦点距離 [mm]
F:F値 [-]
D: センサーと被写体(フォーカス位置)の距離 [mm]
X : 被写体と背景(ぼかすもの)の距離 [mm]
以降フルサイズの話しかしないが、APS-Cでも同じ数値を指標とできるように、上式で得られた錯乱円の径Ysをセンサーの対角長 [mm]で割ったものを錯乱円(相対)Yとする。つまり、これが定量的なボケ量である。
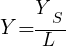
L:センサーの対角長 [mm]
フルサイズでの許容錯乱円をセンサー平面上で0.03 [mm]とすると、許容錯乱円(相対)は0.0007(= 0.03 [mm] / 43 [mm])となる。これ以下はフォーカスが合っている範囲であり、ボケとは認識されない。ちなみにこの数値は甘めなので、厳しく見るならこの半分でもいい。実際、以前の記事では許容錯乱円(相対)を0.00035としていた。
・ボケ量の閾値の仮決め
大きくボケていれば表現上のボケと認識するが、中途半端なボケはフォーカスが甘いだけ(ピンボケ)と認識するのではないかと思う。一概には線引きできないかもしれないが、適当に錯乱円Y<0.005では中途半端なボケ量、Y>0.010ではそれなりの(表現上の)ボケ量とする。大きすぎるボケについては今回は考えない。

上の写真を見ると、錯乱円(相対)Yが0.003だと文字盤のボケがただのピンボケに見えると思う。こんなボケ量なら、ボケていない方がいいのではないか。錯乱円0.006は微妙、0.013になると十分にボケていると見なした。なお、解像度の低いオールドレンズでの絞り開放の例なので、フォーカス位置でもピンボケに見えるのはご愛敬。
上式の通り、YはFLとFとDとXとLの関数であるが、以降FLとFとDとLをそれぞれ固定して、Y = f(X)としてグラフで表示したい。
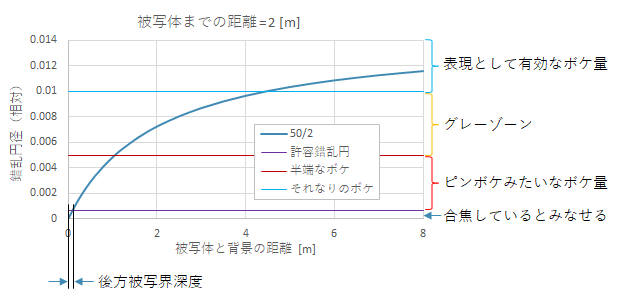
50mm F2(以下50/2のように表記する)のレンズで、被写体に対して2mの距離で撮ったとき、被写体と背景の距離Xと錯乱円径Yの関係は下図のようなカーブとなる。被写体の後方1m程度まではピンボケみたいな中途半端なボケ量となる。被写体の後方4m以上になれば、十分なボケ量となる。その中間はグレーゾーン。
・足ズームとボケ量
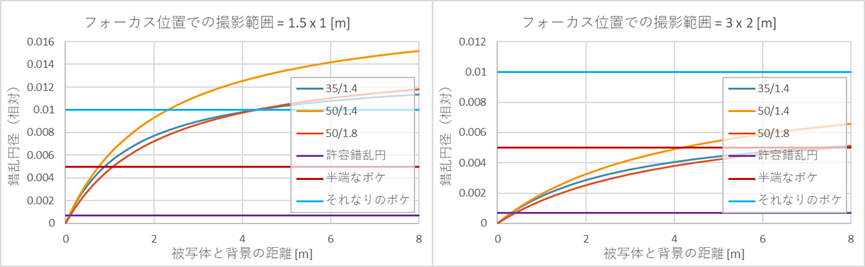
35/1.4と50/1.4と50/1.8のレンズで、足ズーム(被写体に寄る/離れることで写るサイズを変えること)によって同じサイズで被写体を写した際、背景のボケ量がどのようになるかを計算した。
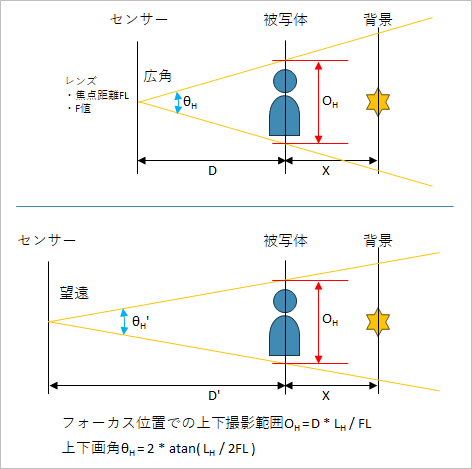
(図中のLHはセンサー上下サイズ=24mm)
35/1.4において、フォーカス位置で写る範囲が1.5 x 1.0 [m]のときと、同じく3.0 x 2.0 [m]のときの2条件に対して、50/1.4と50/1.8で同等の範囲が写るように足ズームした状態を想定している。
この結果、被写体と背景の距離に対する錯乱円は、35/1.4と50/1.8でほぼ同等となっていることが分かる。つまり、この2つのレンズで同じ被写体を同じようなサイズで写したら、背景は同じくらいボケるということである。もちろん画角は違うので、背景の写る範囲は変わってくる。
35/1.4で被写体に寄ったとしても、F1.4といえど、50mmでいうところのF1.8程度しかボケない、と言い換えることもできる。まぁ、実際には十分なボケ量ではあるが。
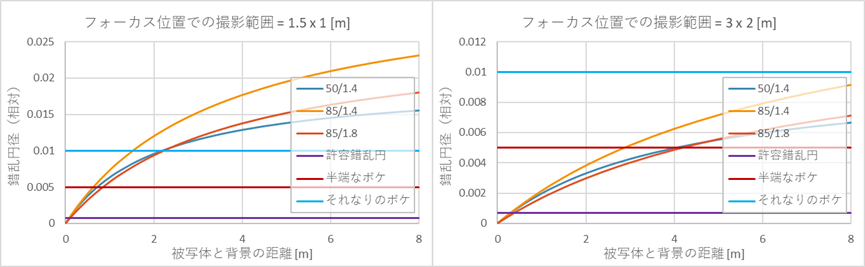
同じように50/1.4と85/1.4と85/1.8でも比較。この場合も50/1.4と85/1.8がほぼ同等であることが分かる。50/1.4で、足ズームを駆使すれば85/1.8に近い程度にはぼかすことができるが、85/1.4との差はそれなりにある。
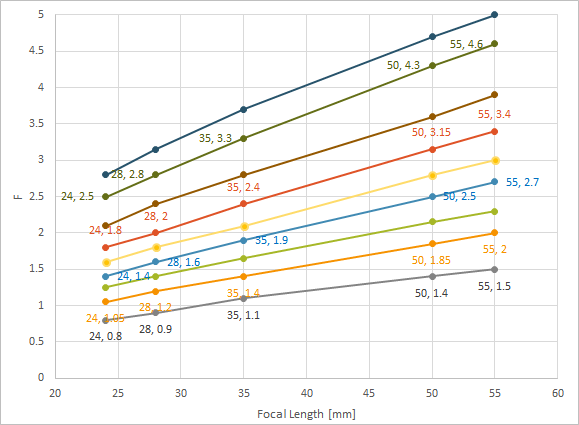
ということで焦点距離とF値で、足ズーム時にボケ量がだいたい等価なライン(わりと目分量)を引いてみた。24mm F1.4なんてすごいスペックでも、ボケ量は50mm F2.5相当でしかない。単焦点レンズにボケを期待するなら、この青色の50mm F2.5が属するラインよりは下にいてほしいものだ。
・広角のF値とボケ量
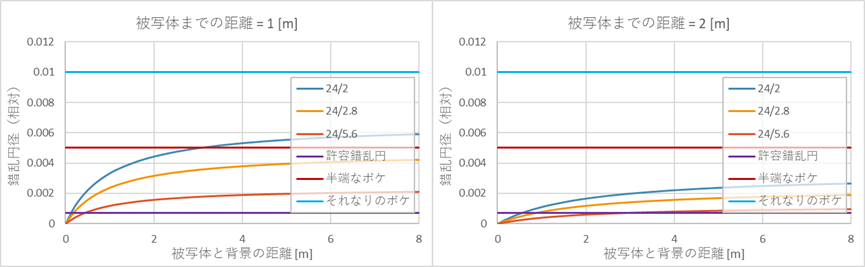
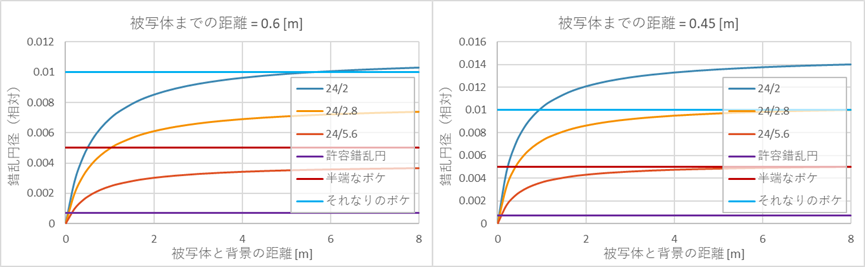
24/2(大口径単焦点)と24/2.8(大口径ズーム)と24/5.6(小口径ズーム ≒ APS-CでF4)でも同様に比較する。
下図の左のように焦点距離24mmでは被写体に1mまで寄ったとき(フォーカス位置で1.5 x 1.0 [m]の範囲が写る)、F2であっても表現上有効なボケ量は得られない。
下図の右のように2mも離れてしまえば、F2やF2.8で撮ってもピンボケにしかならないので、F8やF11まで絞って許容錯乱円以下にした方が好ましいのではないかという状態になる。
焦点距離24mmで、被写体との距離が60cm以内(下図の左)で頻繁に撮影するのであれば開放F2の価値もあるのかもしれないが、また45cm以内(下図の右)で頻繁に撮影するのであれば開放F2.8の価値もあるのかもしれないが、そうでないなら広角の開放F値は暗くていい、と言えるだろう。
24mmよりもさらに広角になれば、なおさらである。
出た、いつもの大口径広角レンズ不要論。
机上で考えただけで、検証はしていないので、計算は間違っているかもしれない。